

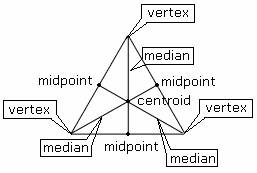
It is possible for a data set to be multimodal, meaning that it has more than one mode. Sommerville, D.M.Y.: An Introduction to the Geometry of N Dimensions. In statistics, the mode is the value in a data set that has the highest number of recurrences. Prasolov, V.V., Tikhomirov, V.M.: Geometry. Peterson, M.A.: The geometry of Piero della Francesca. Ostermann, A., Wanner, G.: Geometry by Its History. Martini, H., Weissbach, B.: Napoleon’s theorem with weights in n-space. Liberti, L., Lavor, C., Maculan, N., Mucherino, A.: Euclidean distance geometry and applications. So if G is the centroid, then: A G 2 3 A D, C G 2 3 C F, E G 2 3 B E D G 1 3 A D, F G 1 3 C F, B G 1 3 B E And by substitution: D G 1 2 A G, F. Lawes, C.P.: Proof without words: the length of a triangle median via the parallelogram law. The Median Theorem states that the medians of a triangle intersect at a point called the centroid that is two-thirds of the distance from the vertices to the midpoint of the opposite sides.
Krantz, S.G., McCarthy, J.E., Parks, H.R.: Geometric characterizations of centroids of simplices.
Johnson, R.A.: Advanced Euclidean Geometry. Izumi, S.: Sufficiency of simplex inequalities. Hungerbühler, N.: Proofs without words: the area of the triangle of the medians has three-fourths the area of the original triangle. This can be done by first constructing a perpendicular bisector. Honsberger, R.: Episodes in Nineteenth and Twentieth Century Euclidean Geometry. This tutorial introduces you to the median of a triangle and shows you how many medians each triangle has Keywords: definition median median triangle. A median of a triangle is a line segment from a vertex to the midpoint of the opposite side. Hersh, R.: Heron’s formula: what about a tetrahedron? Coll. Heath, T.L.: The Thirteen Books of Euclid’s Elements, 2nd edn. Hajja, M., Walker, P.: The Gergonne and Nagel centers of a tetrahedron. Hajja, M., Martini, H., Spirova, M.: New extensions of Napoleon’s theorem to higher dimensions. Hajja, M.: The Gergonne and Nagel centers of an n-dimensional simplex. Gerber, L.: The orthocentric simplex as an extreme simplex. solution, ibid, 86, 387 (2013)įiedler, M.: Isodynamic systems in Euclidean spaces and an n-dimensional analogue of a theorem by Pompeiu. 76, 193–203 (2003)Įdmonds, A.L., Hajja, M., Martini, H.: Coincidences of simplex centers and related facial structures. 68, 914–917 (1961)Ĭrabb, R.A.: Gaspard Monge and the Monge point of the tetrahedron. Springer, Berlin (1994)īlumenthal, L.M.: A budget of curiosa metrica. XYZ Press, LLC (2016)īalk, M.B., Boltyanskij, V.G.: Geometry of Masses. (1964)Īndreescu, T., Korsky, S., Pohoata, C.: Lemmas in Olympiad Geometry. 125, 612–622 (2018)Īl-Afifi, G., Hajja, M., Hamdan, A., Krasopoulos, P.T.: Pompeiu-like theorems for the medians of a simplex. In a triangle, median is a line segment joining a vertex to the midpoint of the corresponding opposite side. Springer, Berlin (2004)Īl-Afifi, G., Hajja, M., Hamdan, A.: Another n-dimensional generalization of Pompeiu’s theorem. It is also called the 50 percent income, which means half of the employees work above this median salary, while half of them work below it.

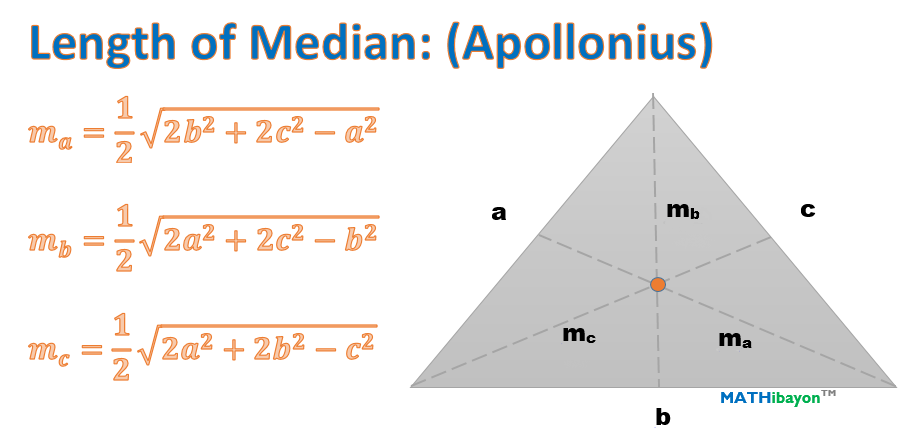
Median salary enables employees to identify the middle point of their salaries in their careers. 51, 466–519 (2014)Īigner, M., Ziegler, G.M.: Proofs from THE BOOK, 3rd edn. The median formula is applied in the workplace to calculate the median salary that sets a reference. According to the theorem: ‘the sum of the squares of any two sides of a triangle equals twice the square on half the third side and twice the square on the median bisecting the third side’.Abrosimov, N.V., Makai Jr., E., Mednykh, A.D., Nikonorov, Y.G., Rote, G.: The infimum of the volumes of convex polytopes of any given facet areas is 0. The Median Theorem states that the medians of a triangle intersect at a point called the centroid that is two-thirds of the distance from the vertices to the midpoint of the opposite sides.
#MEDIAN GEOMETRY HOW TO#
Thus, the 3 medians divide the main triangle into 6 smaller triangles having equal area median AD forms triangles △ABD and △ACD, median BF into △ABF and △CBF, and median CE into △CAE and △CBEįormulas How to Find the Median of a TriangleĪ theorem called Apollonius’s Theorem gives the length of the median of a triangle.


 0 kommentar(er)
0 kommentar(er)
